World Cup Probability Quirks

Group F

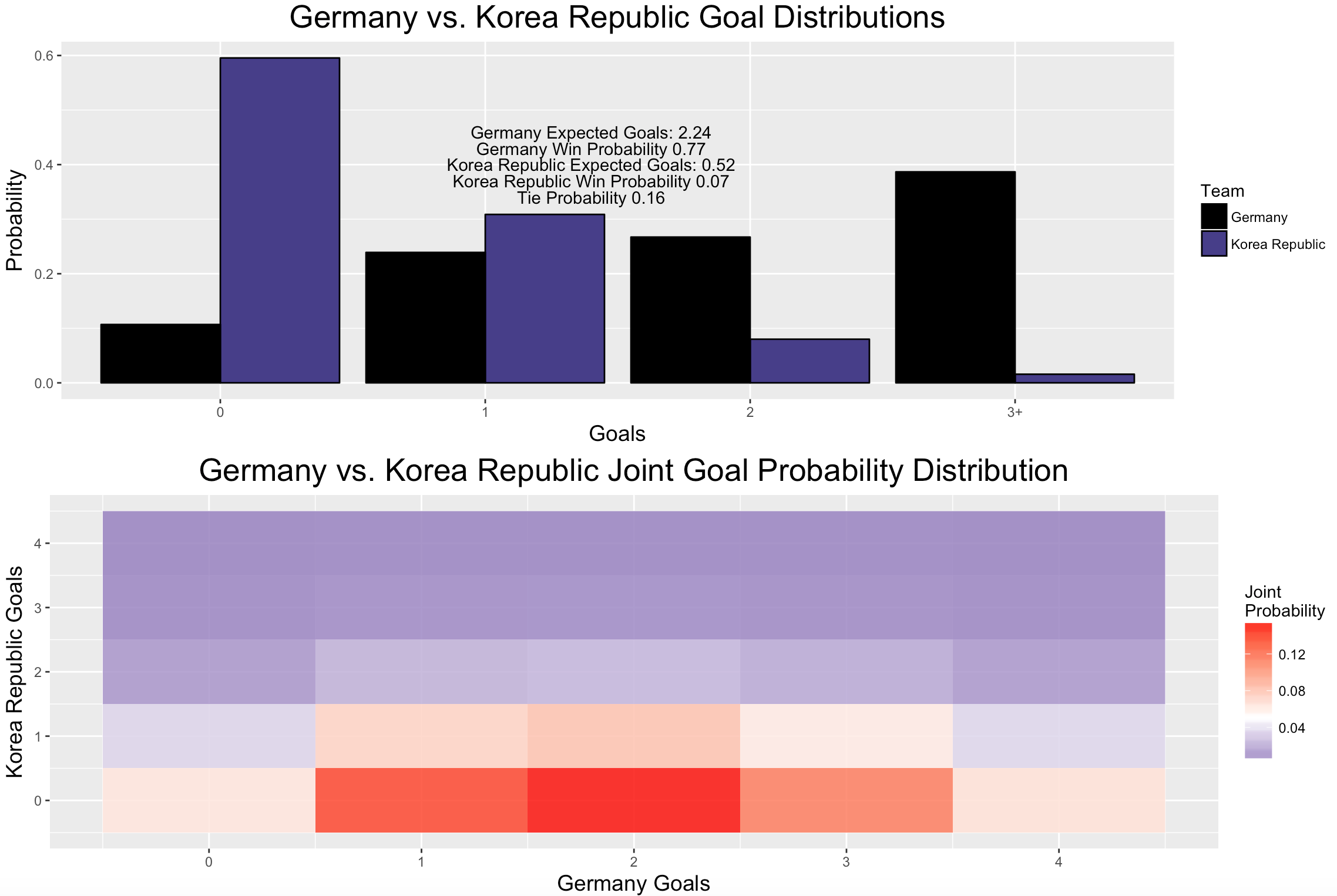
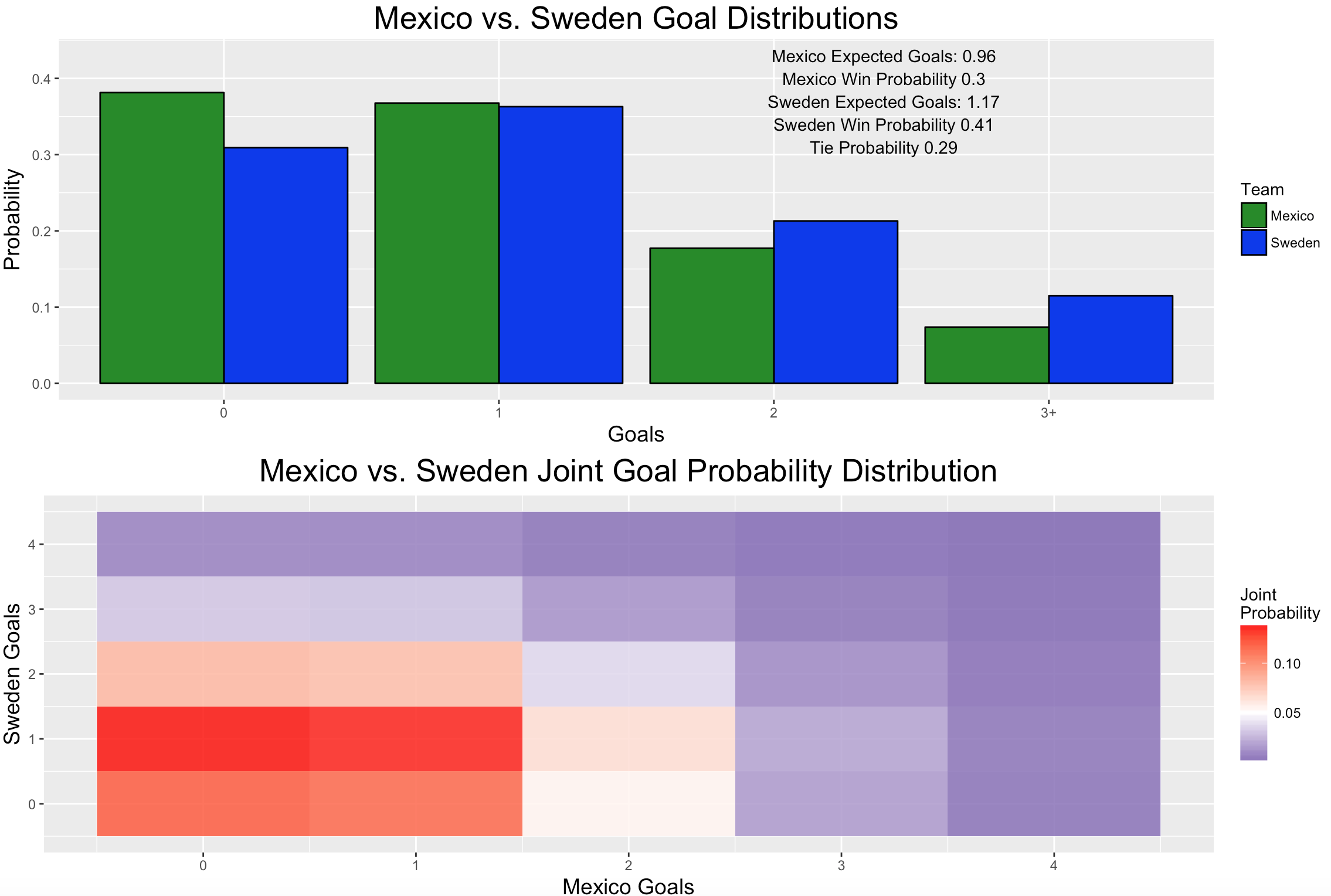
After Toni Kroos’ last gasp winner over Sweden, it’s not exactly groundbreaking to suggest that Group F, comprised of Mexico, Germany, Sweden, and South Korea, will offer one of most exciting endings of any group. All four teams are still alive heading into the final round of matches, meaning everyone’s best squad will be on display. Yet, that’s not the primary reason this group caught my eye. Rather, Group F really caught my eye when I looked at the group standings after 10,000 simulations.

##          country group expected_pts first_in_group second_in_group    r16
## 1        Germany     F         5.48         0.2164          0.6196 0.8360
## 2         Mexico     F         7.24         0.6055          0.1071 0.7126
## 3         Sweden     F         4.47         0.1781          0.2541 0.4322
## 4 Korea Republic     F         0.36         0.0000          0.0192 0.0192

Interestingly, despite leading the group with 6 points, Mexico does not possess the best chance to advance, and frankly, it’s not really that close. According to my model, Germany is about 13% more likely to move on than Mexico. FiveThirtyEight founder Nate Silver noted the same quirk on Twitter. What makes this really interesting, is that Mexico is nearly 3 times as likely as Germany to win thr group, and get roughly 1.7 more points than Germany on average. How is this possible? It all boils down to conditional probability. First, recall the law of total probability. If \(A\) is an event, and \(B_1, ..., B_n\) are a disjoint parition of the of the sample space, then \[ \mathbb{P}(A) = \sum_{i = 1}^n \mathbb{P}(A|B_i) \times \mathbb{P}(B_i) \] In the contest of the World Cup, we can think of \(A\) as being the event that Mexico advances, and \(B_1, B_2\), and \(B_3\) being the events that Mexico wins, ties, or loses its final match against Sweden. Then, we have \[ \mathbb{P}(\text{Mexico Advances}) = \mathbb{P}(\text{Mexico Advances }|\text{ win}) \times \mathbb{P}(\text{win}) + \mathbb{P}(\text{Mexico Advances }|\text{ tie}) \times \mathbb{P}(\text{tie}) + \mathbb{P}(\text{Mexico Advances }|\text{ loss}) \times \mathbb{P}(\text{loss}) \]

Mexico is guarteed to win the group with a win or a tie against Sweeden, so \(\mathbb{P}(\text{Mexico Advances }|\text{ win}) = \mathbb{P}(\text{Mexico Advances }|\text{ tie}) = 1\). With a loss however, Mexico’s position is much more precarious. Full scernarious are outlined here, and Mexico can still advance with a loss, but accoring to my simulations, \(\mathbb{P}(\text{Mexico Advances }|\text{ loss})\) is only about 25%. Conditional on the fact that Mexico loses, they would lose any head to head tiebreaker Sweden, meaning a Germany win over South Korea would almost certainly eliminate El Tri. As for Germany’s favorable odds, a simple look at the expected goal distirbution for the final two matches expain why my model suggests Mexico isn’t as safe as one might’ve thought.

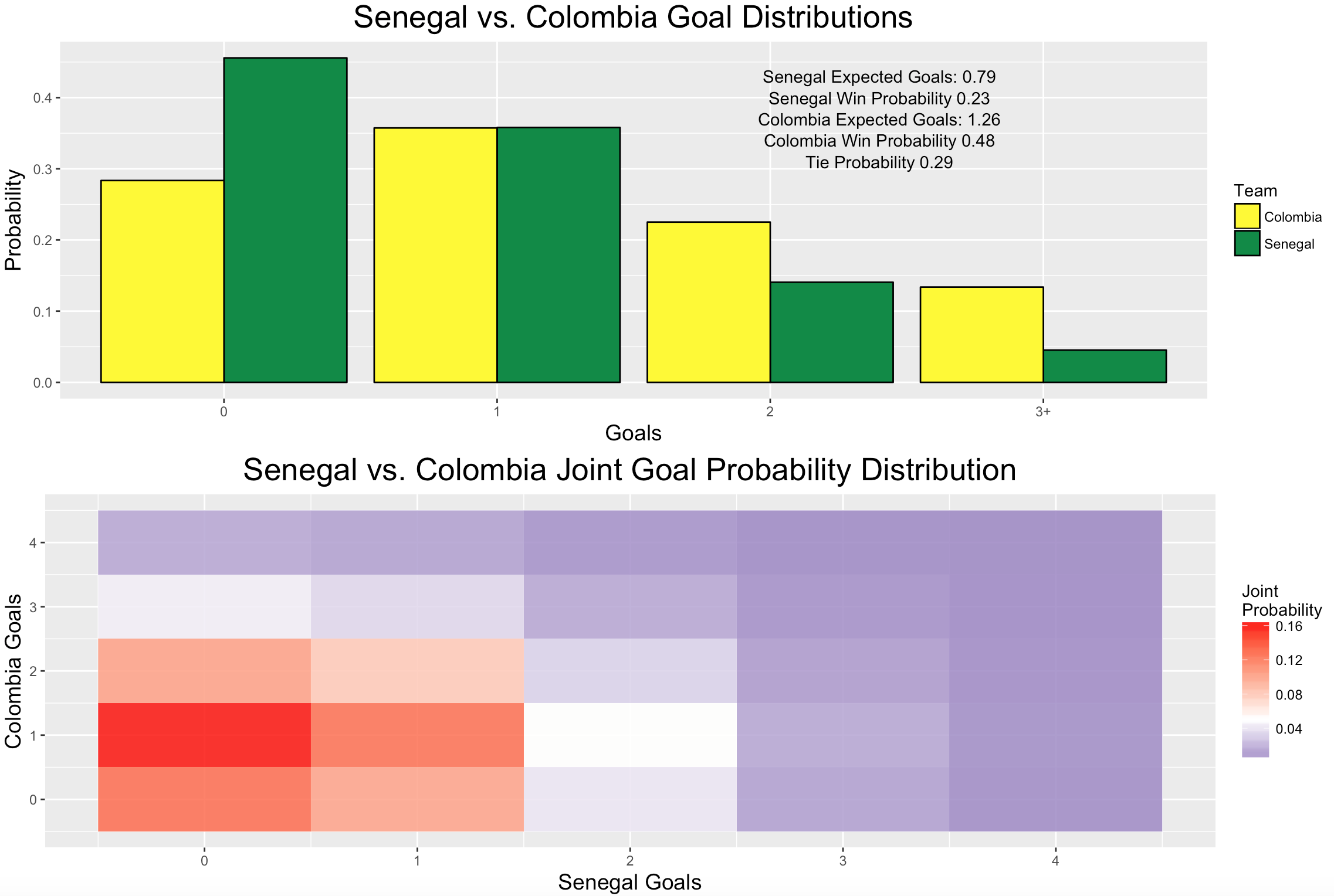
Group H

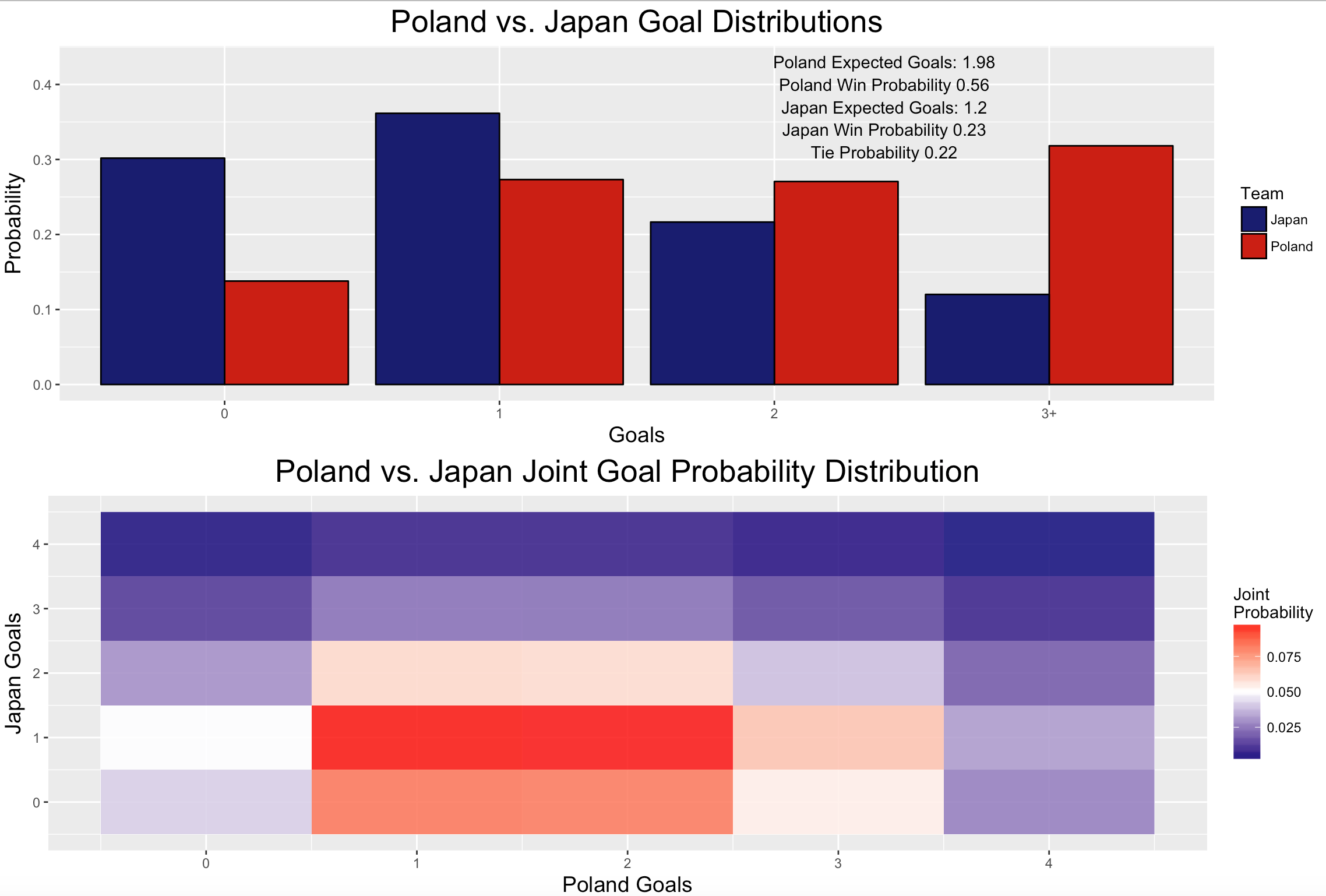
The other interesting group from a probability standpoint is Group H, comprised of Senegal, Poland, Japan, and Colombia. While Poland has been elimanted from the World Cup, the other three squads have a good will fight on the final match day for two spots in the knockout round. Here’s how the simulations see the group shaking out.

##    country group expected_pts first_in_group second_in_group    r16
## 1  Senegal     H         5.94         0.5168          0.2633 0.7801
## 2    Japan     H         4.71         0.2340          0.2608 0.4948
## 3   Poland     H         3.36         0.1338          0.2807 0.4145
## 4 Colombia     H         2.91         0.1154          0.1952 0.3106

We see two things about this that are noteworthy.

1. Japan, Senegal, and Colombia are all each more likely to advance than not despite the fact that one of them will not advance.
2. All three of the those countries are essentially a 2/3 chance of advancing.

At first, 1. might seem somewhat paradoxical, but actually it’s quite reasonable. After all \[ \sum_{teams} \mathbb{P}(\text{team advances}) = 2 \] as there are 2 spots in the knockout round for each group. Given that Poland has already been eliminated, we must divide that 200% of probability amongst 3 teams somehow, and doing so in a relatively even manner yields this neat result. Micah McCurdy has a good explanation on this phenomon in general. Perhaps even more interesting is the fact that the three remaining countries’ chances don’t deviate significantly from a true random draw, in which each country’s chances would be exactly 2/3. Any time you have random or near random events in sports, it’s almost always exciting (this is why we find March Madness so appealing, for instance), meaning that Group H’s final matchday will be must-see TV. Here’s how my model sees the final Group H matches.3